| Noir⋅es | Blanc⋅hes | Total | |
| Illettré⋅es | 1 512 000 | 2 406 000 | 3 918 000 |
| Lettré⋅es | 7 780 000 | 85 574 000 | 93 354 000 |
| Total | 9 292 000 | 87 980 000 | 97 272 000 |
Corrélations écologiques et comportement des individus
Introduction
Une corrélation individuelle est une corrélation dont l’objet statistique ou la chose décrite est indivisible1. La corrélation entre la race renseignée2 et l’illettrisme de personnes résidant aux États-Unis, exposée plus loin dans le Tableau 1, est une corrélation individuelle parce que le type de chose décrite est une unité indivisible, une personne. Les variables d’une corrélation individuelle sont des propriétés descriptives des individus, telles que la taille, le revenu, la couleur des yeux ou la race renseignée, et non des constantes statistiques descriptives telles que des taux ou des moyennes.
Avec une corrélation écologique, l’objet statistique est un groupe de personnes. La corrélation entre le pourcentage de la population qui est renseignée comme noire et le pourcentage de la population qui est illettrée pour les 48 États des États-Unis, exposée plus loin dans le Tableau 2, est une corrélation écologique. La chose décrite est la population d’un État, et non un individu unique. Les variables sont des pourcentages, des propriétés descriptives de groupes, et non des propriétés descriptives d’individus.
Les corrélations écologiques sont utilisées dans un nombre impressionnant d’études sociologiques quantitatives, dont certaines ont acquis le statut de classiques : celle d’Alfred Cowles sur les liens entre climat et tuberculose (Cowles et Chapman, 1935) ; les études d’Harold F. Gosnell sur le vote aux élections présidentielles à Chicago en 1932 (Gosnell et Gill, 1935), son analyse factorielle et corrélationnelle du vote de 1934 à Chicago (Gosnell et Schmidt, 1936) et l’analyse factorielle plus élaborée qu’il a présentée dans son livre sur les « machines politiques » à Chicago (Gosnell, 1938) ; les études de William F. Ogburn sur le vote des femmes (Ogburn et Goltra, 1919), sur les facteurs du vote aux élections présidentielles de 1928 (Ogburn et Snow, 1929), sur les facteurs du crime dans les villes (Ogburn, 1935) ainsi que son livre co-écrit avec Ernest R. Groves sur les relations familiales et le mariage aux États-Unis (Groves et Ogburn, 1928) ; l’étude de Frank A. Ross sur l’assiduité scolaire au Texas (Ross, 19243) ; les études coordonnées par Clifford R. Shaw sur la répartition géographique de la délinquance à Chicaco (Shaw et al, 1922 ; Shaw et al, 1942) ; l’étude de Warren S. Thompson sur les facteurs du nombre d’enfants par femme dans les villes étatsuniennes en 1930 (Thompson, 1939) ; l’étude de Pascal K. Whelpton sur les corrélats géographiques et économiques du taux de naissance (Whelpton, 1936) ; et l’étude de R. Clyde White sur les facteurs environnementaux du crime à Indianapolis (White, 1932).
Si ces études et d’autres semblables reposent sur des corrélations écologiques, ce n’est pas parce que leurs auteurices s’intéressent aux corrélations entre les propriétés des territoires étudiés en tant que tels. Même les écologistes pur⋅es et dur⋅es, quand iels étudient par exemple la délinquance, s’appuient principalement sur des données décrivant des individus, et non des territoires4. Dans chaque enquête qui mobilise les corrélations écologiques, l’objectif évident est de découvrir quelque chose à propos du comportement des individus. Il est fait recours aux corrélations écologiques simplement parce que les corrélations entre les propriétés des individus ne sont pas disponibles. Pourtant, dans chacun de ces cas, la substitution n’est pas explicitée.
Le but de cet article est de clarifier le problème de la corrélation écologique en établissant mathématiquement la relation exacte entre les corrélations écologiques et individuelles et en montrant l’incidence qu’a cette relation sur l’usage des corrélations écologiques comme substituts des corrélations individuelles.
Anatomie d’une corrélation écologique
Cependant, avant d’aborder cette relation mathématique, il est nécessaire d’exposer le lien structurel entre corrélations écologiques et individuelles dans une situation spécifique. La Figure 1 montre le diagramme de dispersion de la corrélation écologique entre la race renseignée et l’illettrisme pour les neuf divisions géographiques des États-Unis établies par le recensement de 1930. La coordonnée X de chaque point est le pourcentage de la population de la division âgée de 10 ans et plus qui est renseignée comme noire. La coordonnée Y est le pourcentage de cette même population qui est illettrée5. La corrélation de Pearson pour la Figure 1, c’est-à-dire la corrélation écologique, est de 0,946.

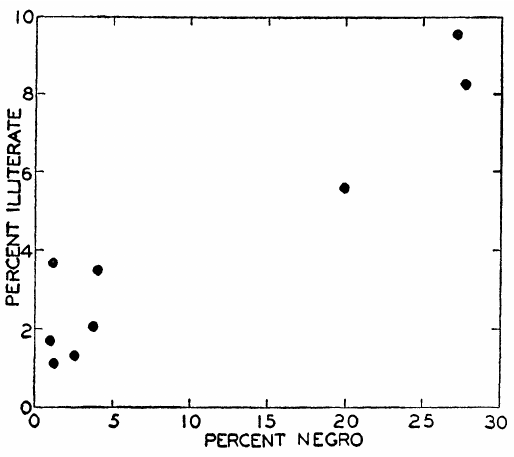
Le Tableau 1 est un tableau 2x26 qui montre, pour la même population, la corrélation entre la race renseignée et l’illettrisme considérés comme des propriétés des individus plutôt que des zones géographiques. Le coefficient phi7 pour le Tableau 1, c’est-à-dire la corrélation individuelle, est de 0,203, soit un peu plus qu’un cinquième de la corrélation écologique correspondante.
D’ordinaire, une telle corrélation écologique serait calculée à l’échelle du comté ou de l’État, et non à l’échelle des divisions du recensement choisie ici pour simplifier la visualisation numérique. Mais les résultats sont similaires quelles que soient les zones écologiques retenues, comtés, États ou divisions. La Figure 2 montre par exemple la corrélation écologique à l’échelle de l’État et non de la division. Elle s’élève alors à 0,773, à comparer aux 0,946 obtenus quand l’échelle écologique est celle des divisions.

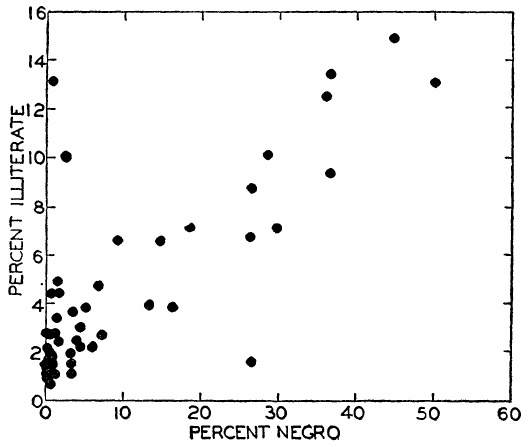
Le lien entre la corrélation individuelle du Tableau 1 et la corrélation écologique de la Figure 1 repose sur les corrélations individuelles entre la race renseignée et l’illettrisme à l’intérieur des neuf divisions géographiques, qui fournissent les neuf observations pour la corrélation écologique. Il s’agit donc des corrélations individuelles intra-zones écologiques, dont une sélection est présentée dans le Tableau 2.
| Noir⋅es | Blanc⋅hes | Total | ||
| New England | Illettré⋅es | 4 000 | 240 000 | 244 000 |
| Lettré⋅es | 72 000 | 6 386 000 | 6 458 000 | |
| Total | 76 000 | 6 626 000 | 6 702 000 | |
| Middle Atlantic | Illettré⋅es | 32 000 | 719 000 | 751 000 |
| Lettré⋅es | 836 000 | 19 958 000 | 20 794 000 | |
| Total | 868 000 | 20 677 000 | 21 545 000 | |
| East North Central | Illettré⋅es | 36 000 | 392 000 | 428 000 |
| Lettré⋅es | 735 000 | 19 443 000 | 20 178 000 | |
| Total | 771 000 | 19 835 000 | 20 606 000 | |
| Pacific | Illettré⋅es | 2 000 | 71 000 | 73 000 |
| Lettré⋅es | 75 000 | 6 332 000 | 6 407 000 | |
| Total | 77 000 | 6 403 000 | 6 480 000 |
La corrélation individuelle et la corrélation écologique dépendent toutes deux des corrélations individuelles intra-zones écologiques, mais de manières différentes. La corrélation individuelle (Tableau 1) dépend des fréquences internes, soit les fréquences renseignées dans les cases du Tableau 2 des neuf corrélations individuelles intra-zones écologiques. Les fréquences indiquées dans chacune des cases sont la somme des neuf fréquences correspondantes à l’échelle des divisions. Par exemple, la fréquence 1 512 000 de la première case du Tableau 1 est la somme des fréquences 4 000 + 32 000 + 36 000 + 2 000 + … du Tableau 2.
La corrélation écologique (Figure 1) dépend elle aussi des neuf corrélations individuelles intra-zones écologiques, mais uniquement de leurs effectifs marginaux. Par exemple, dans le Tableau 2, l’effectif marginal indique 76 000 noir⋅es pour la division New England. La population totale de cette division étant de 6 702 000, le pourcentage de noir⋅es est 100*76 000/6 702 000 = 1,1 %. Le pourcentage d’illettré⋅es au sein de la division New England est calculé de la même façon à partir de l’autre effectif marginal.
En bref, la corrélation individuelle dépend des fréquences internes des corrélations individuelles intra-zones écologiques, alors que la corrélation écologique dépend des fréquences marginales des corrélations individuelles intra-zones écologiques. De plus, il est bien connu que les fréquences marginales d’un tableau 2x2 ne déterminent pas les fréquences internes. On peut trouver un grand nombre d’ensembles de fréquences internes qui satisfont exactement les mêmes fréquences marginales pour tout tableau 2x2. Par conséquent, il existe un grand nombre de corrélations individuelles qui pourraient correspondre à toute corrélation écologique donnée, c’est-à-dire à tout ensemble d’effectifs marginaux. En résumé, les fréquences marginales intra-zones écologiques qui déterminent les pourcentages à partir desquels est calculée la corrélation écologique ne déterminent pas les fréquences internes qui déterminent la corrélation individuelle. De ce fait, il n’y a pas nécessairement de correspondance entre la corrélation individuelle et la corrélation écologique.
Un exemple permettra d’illustrer cette conclusion. Les données présentées montrent que la corrélation individuelle entre la race renseignée et l’illettrisme est de 0,203, alors que la corrélation écologique est de 0,946. Dans ce cas, les deux corrélations ont le même signe, et ce signe est cohérent avec notre connaissance du fait que les taux d’éducation aux États-Unis sont plus bas pour les noir⋅es que pour les blanc⋅hes.
Cependant, considérons une autre corrélation pour laquelle nous savons également ce que le signe devrait être, à savoir celle entre le lieu de naissance et l’illettrisme. On sait que les taux d’éducation sont plus bas pour les personnes nées à l’étranger que pour celles nées aux États-Unis, si bien qu’on devrait observer une corrélation positive entre la naissance à l’étranger et l’illettrisme. Cette hypothèse est corroborée par la corrélation individuelle entre la naissance à l’étranger et l’illettrisme, présentée dans le Tableau 3, qui est de 0,118.
| Né⋅e à l’étranger | Né⋅e aux États-Unis | Total | |
| Illettré⋅es | 1 304 000 | 2 614 000 | 3 918 000 |
| Lettré⋅es | 11 913 000 | 81 441 000 | 93 354 000 |
| Total | 13 217 000 | 84 055 000 | 97 272 000 |
Pourtant, la corrélation écologique entre la naissance à l’étranger et l’analphabétisme, présentée dans la Figure 3, est de -0,619 ! Lorsque la corrélation écologique est calculée à l’échelle des États plutôt qu’à celle des divisions, sa valeur est de -0,526.

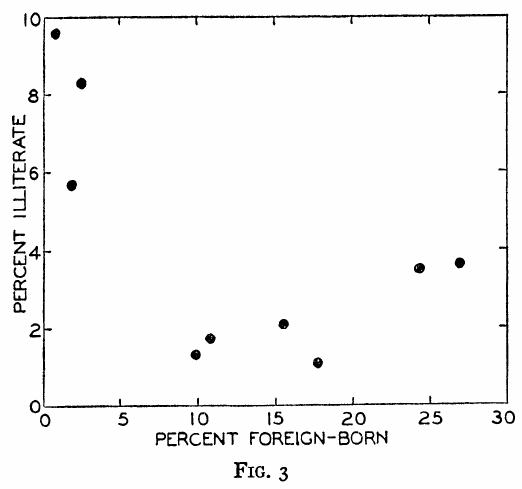
La relation mathématique entre les corrélations écologique et individuelle
Les corrélations individuelle et écologique, de même que d’autres corrélations qui jouent aussi un rôle dans la situation, sont fonctionnellement liées par l’une des équations basiques de l’analyse de covariance10. Cette équation peut être construite à partir des hypothèses suivantes, qui se contentent de décrire en termes mathématiques la situation sous-jacente à une corrélation écologique :
- Il existe un groupe de N personnes caractérisées par deux variables de propriétés X et Y. Ces propriétés peuvent être des variables continues, telles que l’âge ou le revenu, ou des attributs dichotomiques, tels que le sexe ou l’alphabétisation.
- Les N membres du groupe peuvent être distribués dans m sous-groupes distincts en fonction de leur localisation géographique, qu’il s’agisse de secteurs du recensement, de cantons, de comtés ou d’États. On conçoit ces m sous-groupes comme définis par les m valeurs d’une troisième variable Z (zone), qui est réellement un attribut, en l’espèce une région géographique.
Les valeurs numériques à partir desquelles la corrélation écologique est calculée décrivent ces m sous-groupes. Elles peuvent consister en moyennes, en médianes ou en pourcentages, et en réalité les trois sont parfois mobilisées dans une même analyse de corrélation écologique. Cependant, il s’agit le plus souvent de pourcentages. Même si l’argument mathématique s’applique tout aussi bien aux moyennes, et approximativement aux médianes, il sera plus simple pour le présent propos de considérer que X et Y sont des propriétés dichotomiques et que, par conséquent, la corrélation écologique est une corrélation entre des paires de pourcentages.
Dans la section précédente, on a montré que trois corrélations distinctes étaient impliquées par la corrélation écologique. En termes mathématiques, ces corrélations sont décrites comme suit.
La corrélation individuelle totale (r) est la simple corrélation de Pearson entre X et Y pour tous les N membres du groupe complet, calculée sans référence à la position géographique. Si X et Y sont des propriétés dichotomiques, la corrélation individuelle totale sera le coefficient phi du tableau 2x2 (Tableau 1).
La corrélation écologique (re) est la corrélation pondérée entre les m paires de pourcentages X et de pourcentages Y qui décrivent les sous-groupes. Dans l’exemple donné plus haut, re est la corrélation entre les neuf pourcentages de noir⋅es et les pourcentages correspondants d’illettré⋅es. Cependant, chaque résultat du croisement d’un pourcentage X et d’un pourcentage Y est pondéré par le nombre de personnes au sein du groupe que le pourcentage décrit, afin de lui donner une importance relative au nombre d’observations impliquées.
D’ordinaire, les corrélations écologiques sont calculées sans recourir au raffinement de la pondération. Bien que la forme pondérée est théoriquement plus pertinente, et est requise pour les mathématiques de cette section, la différence numérique qu’elle produit est négligeable. Ainsi, la corrélation écologique pondérée de la Figure 1, qui implique peu d’observations et devrait donc être sensible à la pondération, est de 0,946, alors que la valeur non pondérée correspondante est de 0,944.
La corrélation individuelle intra-zones (rw) est une moyenne pondérée des m corrélations individuelles intra-zones entre X et Y, chaque corrélation interne aux zones étant pondérée par la taille du groupe qu’elle décrit.
Deux rapports de corrélation, ηXA et ηYA, sont aussi impliqués dans la relation. Ils servent à mesurer le degré auquel les valeurs de X et de Y diffèrent d’une zone à l’autre. Si X est une propriété dichotomique, par exemple l’illettrisme, alors une valeur élevée de ηXA indique une forte variation du pourcentage d’illettré⋅es d’une zone à l’autre.
À partir de ces définitions, la relation entre les corrélations individuelle et écologique peut être écrite ainsi :
(1)
où
(1a)
et
(1b)
Autrement dit, la corrélation écologique est la différence pondérée entre la corrélation individuelle totale et la moyenne des m corrélations individuelles intra-zones. Pour cette différence pondérée, les poids respectifs de la corrélation individuelle totale et de la corrélation individuelle intra-zones dépendent du degré auquel les valeurs de X et de Y sont différentes d’une zone à l’autre.
L’analyse de la relation donnée en (1) montre que des corrélations individuelle et écologique seront égales, et que par conséquent l’hypothèse d’équivalence sera valide, quand
(2)
où
(2a)
La valeur minimale de k3 dans (2) est l’unité. De ce fait, (2) sera valable, et les corrélations individuelle et écologique seront égales, si la moyenne des corrélations individuelles intra-zones ne vaut pas moins que la corrélation individuelle totale. Mais toutes les preuves disponibles montrent que, quoi qu’indiquent les propriétés X et Y, la corrélation entre X et Y n’est certainement pas plus importante pour des sous-groupes relativement homogènes que pour la population dans son ensemble. En bref, l’hypothèse d’équivalence n’a aucune base factuelle. Il doit alors exister une raison pour laquelle les valeurs des corrélations écologiques publiées sont systématiquement élevées en comparaison des valeurs plus petites qu’on obtient habituellement en calculant les corrélations entre les propriétés individuelles. La relation présentée en (1) l’indique : elle donne la condition d’une valeur numérique plus élevée de la relation écologique
(3)
où k3 est donné par (2a). Comme la valeur minimale de k3 est l’unité, l’équation (3) implique que la corrélation écologique sera numériquement plus élevée que la corrélation individuelle quand la corrélation individuelle intra-zones n’est pas plus élevée que la corrélation individuelle totale, ce qui est le cas habituellement.
Les personnes qui utilisent les corrélations écologiques savent que la taille du coefficient dépend fortement du nombre de zones. Gehlke et Biehl, par exemple, ont commenté en 1934 la relation positive entre la taille du coefficient et la taille moyenne des zones à partir desquelles il était calculé (Gehlke et Biehl, 1934). Cette tendance est illustrée par les exemples donnés plus haut : la corrélation entre la race renseignée et l’illettrisme est de 0,773 quand les zones sont les États et de 0,946 quand les zones sont les neuf divisions géographiques du recensement. La même tendance est manifestée par les corrélations entre le lieu de naissance et l’illettrisme, dont la valeur est de -0,526 quand il s’agit des États et de -0,619 quand il s’agit des divisions.
L’équation (1) montre pourquoi la taille de la corrélation écologique dépend du nombre des zones. C’est que le comportement de la corrélation écologique dès lors que de petites zones sont regroupées dans de plus larges peut être prédit à partir du comportement des variables à la droite de (1) quand l’agrégation est effectuée. Quand les petites zones sont agrégées, il arrive deux choses :
- La corrélation individuelle intra-zones moyenne augmente du fait de l’accroissement de l’hétérogénéité des zones. Ceci a pour effet de diminuer la valeur de la corrélation écologique.
- Les valeurs de ηXA et ηYA diminuent du fait de la moindre homogénéité des valeurs de X et de Y au sein de chaque zone. Ceci a pour effet d’augmenter la valeur de la corrélation écologique.
Mais ces deux tendances ne sont pas aussi importantes l’une que l’autre. L’analyse de (1) concernant l’effet des changements de valeurs de ηXA, ηYA et rw indique que cet effet est considérablement plus important pour les η que pour rw. L’effet net des changements de ces trois valeurs pris ensemble est donc celui d’un accroissement de la valeur numérique de la corrélation écologique lorsqu’une agrégation des zones est réalisée.
Conclusion
L’étude de la relation entre les corrélations écologique et individuelle fournit une réponse définitive à la question posée en début d’article : les corrélations écologiques peuvent-elles être substituées aux corrélations individuelles ? Non. Même s’il est théoriquement possible que les deux soient égales, les conditions sous lesquelles ceci peut arriver sont très éloignées de celles rencontrées dans les données réelles. D’un point de vue pratique, la seule affirmation raisonnable est qu’une corrélation écologique n’est, avec une certitude presque totale, pas égale à la corrélation individuelle qui lui correspond.
J’ai conscience que cette conclusion a de sérieuses conséquences, et que ses effets semblent entièrement négatifs parce qu’elle jette un sérieux doute sur la validité d’un nombre important de travaux réalisés récemment. Mais l’objectif de cet article sera atteint s’il empêche à l’avenir le calcul de corrélations dénuées de sens et stimule l’étude de problèmes similaires à l’aide de corrélations sensées entre les propriétés des individus.



- 1Traduit par Olivier Roueff. Article original : William S. Robinson, « Ecological Correlations and the Behavior of Individuals », American Sociological Review, vol 15, no3, 1950, p. 351–357.
- 2Ndt : « color » dans l’article original. L’article étant paru en 1950, avant le long et conflictuel processus de réforme du vocabulaire utilisé s’agissant des catégorisations raciales assignées et/ou revendiquées, on s’autorise à transposer les termes originaux dans un langage contemporain, d’autant plus facilement qu’ils concernent seulement des illustrations des arguments au centre du propos de l’auteur, ne modifiant en rien le sens de ces derniers. Ici, « color » n’est donc pas traduit par « couleur de peau » mais par « race renseignée » (dans les questionnaires statistiques) ; plus loin « Negro » est traduit par « noir⋅e » (sans majuscules, comme il est devenu d’usage pour exprimer le souci de ne pas essentialiser les catégories raciales), à l’exception des légendes des deux Figures 1 et 2 puisqu’elles sont reproduites en fac-simile.
- 3 Ndt : l’étude porte en réalité sur tous les États des États-Unis.
- 4Comme dans les études mentionnées sur les zones urbaines de la délinquance coordonnées par Clifford R. Shaw.
- 5Ces pourcentages ont été calculés à partir des effectifs marginaux des tableaux 2x2 rassemblés dans le Tableau 2.
- 6NdT : C’est-à-dire un tableau croisant deux variables binaires, donc à deux lignes et deux colonnes (i.e. quatre cases, Robinson parle d’ailleurs de « fourfold table »).
- 7NdT : Robinson utilise l’expression « Pearsonian fourfold-point correlation », qui n’est plus guère employée, mais correspond au coefficient phi, aussi appelé coefficient de contingence carré moyen. Ce coefficient, introduit par Karl Pearson, mesure l’association entre deux variables binaires. Il est strictement équivalent au coefficient de corrélation linéaire de Pearson appliqué aux deux variables binaires codées en 0 ou 1.
- 8La source de ce tableau et des suivants est le recensement étatsunien de 1930.
- 9Les résultats pour les divisions West North Central, South Atlantic, East South Central, West South Central, Mountain sont omis faute de place.
- 10La dérivation de cette équation n’est pas donnée ici faute de place. Les lecteurices souhaitant en recevoir une copie peuvent envoyer une enveloppe timbrée et auto-adressée à W. S. Robinson, Department of Anthropology and Sociology, University of California, Los Angeles 24, California.
- Cowles Alfred 3rd, Chapman Edward N., 1935, « Statistical Study of Climate in Relation to Pulmonary Tuberculosis », The American Political Science Review, no24, p. 967-984.
- Gehlke C. E., Biehl Katherine, 1934, « Certain Effects of Grouping upon the Size of the Correlation Coefficient in Census Tract Material », Journal of the American Statistical Association, no29, p. 169-170.
- Gosnell Harold F., Gill Norman N., 1935, « An Analysis of the 1932 Presidential Vote in Chicago », The American Political Science Review, vol. 29, no6, p. 967-984.
- Gosnell Harold F., 1938, Machine Politics: Chicago Model, Chicago, University of Chicago Press.
- Gosnell Harold F., Schmidt Margaret J., 1936, « Factorial and Correlational Analysis of the 1934 Vote in Chicago », Journal of the American Statistical Association, vol. 31, no195, p. 507-518.
- Groves Ernest R., Ogburn William F., 1928, American Marriage and Family Relationships, New York, Holt.
- Ogburn William F., 1935, « Factors in the Variation of Crime Among Cities », Journal of the American Statistical Association, vol. 30, no189, p. 12-34.
- Ogburn William F., Goltra Inez, 1919, « How Women Vote », Political Science Quarterly, vol. 34, no3, p. 413-433.
- Ogburn William F., Snow Nell, 1929, « A Measurement of the Factors in the Presidential Election of 1928 », Social Forces, vol. 8, no2, p. 175-183.
- Ross Frank A., 1924, School Attendance in 1920. An Analysis of School Attendance in the United States and in the Several States, With a Discussion of the Factors Involved, Chicago, Government Printing Office.
- Shaw Clifford R., McKay Henry D., Hayner Norman S., Cressey Paul G., Schroeder Clarence W., Sullenger T. Earl, Moses Earl R., Schmid Calvin F., 1942, Juvenile Delinquency and Urban Areas: A Study of Rates of Delinquents in Relation to Differential Characteristics of Local Communities in American Cities, Chicago, Chicago University Press.
- Shaw Clifford R., Zorbaugh Frederick M., McKay Henry D., Cottrell Leonard S., 1929, Delinquency areas: A Study of the Geographic Distribution of School Truants, Juvenile Delinquents, and Adult Offenders in Chicago, Chicago, University of Chicago Press.
- Thompson Warren S., 1939, « Some Factors Influencing the Ratios of Children to Women in American Cities, 1930 », American Journal of Sociology, no45, p. 183-199.
- Whelpton Pascal K., 1936, « Geographic and Economic Differentials in Fertility », The Annals of the American Academy of Political and Social Science, vol. 188, p. 37-55.
- White R. Clyde, 1932, « The Relation of Felonies to Environmental Factors in Indianapolis », Social Forces, vol. 10, no4, p. 498-509.
William S. Robinson